データ分析
前回は不公平なAIシステムの活用事例を紹介し公平性とはどんなものかを概観しました。また、不公平の原因はバイアスにあることを述べ、いくつかのバイアスを紹介しました。
第2部では、いよいよ公平性の定義を扱います。また、いくつかの不公平性の緩和アルゴリズムも紹介します。ここで登場したアルゴリズムの1つを第3部で実際に実装していきますので楽しみにしていてください。
目次
公平性の定義
| 差別名 | 説明 |
|---|---|
| 直接差別 | 個人のセンシティブ属性が明示的に不利益をもたらす差別。 |
| 間接差別 | センシティブ属性ではないが暗黙的に不利益をもたらす差別。 例）郵便番号はその土地に住む人種と相関する可能性がある。 |
| 組織的差別 | 政治、慣習および文化に起因する差別。 例）雇用者は共通の文化や経験をもつ者を好んで採用する。 |
| 統計的差別 | 意思決定者が集団の統計量を用いてその集団に属する個人を判断するときに生じる差別。 |
| 説明可能な区別 | グループ間での結果の相違をある属性を介して正当化できる区別。 例）UCI Adult datasetを分析すると男性の方が女性よりも平均的に高い年収を得ていることが分かります。しかし、これは労働時間に影響するものであり年収の差異は正当化される。また、労働時間を考慮せず、これを差別とすると男性の時間給を減少させるような逆差別が起こりうる。 |
| 説明不可能な差別 | 正当化できない差別。 |
| 公平性の大分類 | 説明 |
|---|---|
| 個人の公平性 | 類似の個人には類似の予測を与える。 |
| グループの公平性 | センシティブ属性に依らず対象変数の分布は等しい。 |
| 公平性の規準 | 公平性の大分類 |
|---|---|
| 等価オッズ | グループの公平性 |
| 機会均等 | グループの公平性 |
| デモグラフィックパリティ | グループの公平性 |
| 認識を通した公平 | 個人の公平性 |
| 無意識による公平 | 個人の公平性 |
| 条件付き統計的公平 | グループの公平性 |
以下では、2値分類に話題を絞って公平性の定義を紹介しよう。その際、以下の記号を用います。
$X$：非センシティブ属性
$A in $ {0,1}：センシティブ属性
$Y in $ {0,1}：目的変数
$hat{ Y } in $ {0,1} or $R$（実数）：予測ラベル or 予測スコア（主に確率値）
■公平性の定義：デモグラフィックパリティ
事例：Instant Checkmate社のネット広告
米国の逮捕歴の情報などを検索するサイトであるInstant Checkmate社によるネット広告に関するSweeneyによる報告によれば、アフリカ系の名前でGoogle検索をすると、その人物が「逮捕されたか？」という逮捕歴を示唆する広告が表示されやすい。一方、ヨーロッパ系の名前で検索すると、逮捕歴を示唆しない中立的な広告が表示されます。人種により表示する広告が異なる原因は、クリック数を最大化するモデルが採用されたためでした。データ分析技術自体に恣意的な偏見はないが、データが含有する社会的悪意（アフリカ系の名前に対しては逮捕歴に関する広告を表示するとクリックされやすい）が意図せず反映されてしまった結果、このような問題が生じました。検索サイトにネガティブな広告が度々登場するのは不快ですし、それが特定の人種にだけ起こり得るというのも問題です。したがって、人種間での表示される広告の割合を一定に保ちたくなります。このタイプの公平性の規準がデモグラフィックパリティと呼ばれるものです。 定義（デモグラフィックパリティ）： 予測ラベル$hat{ Y } $、センシティブ属性$A$に対して、 $P(hat{ Y } = 1| A = 1) = P(hat{ Y } = 1| A= 0)$ …（予測確率の相等） が成り立つとき、デモグラフィックパリティを満たすという。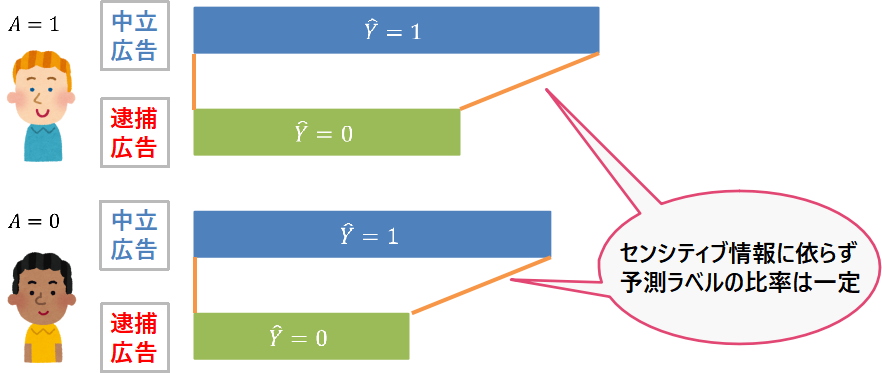
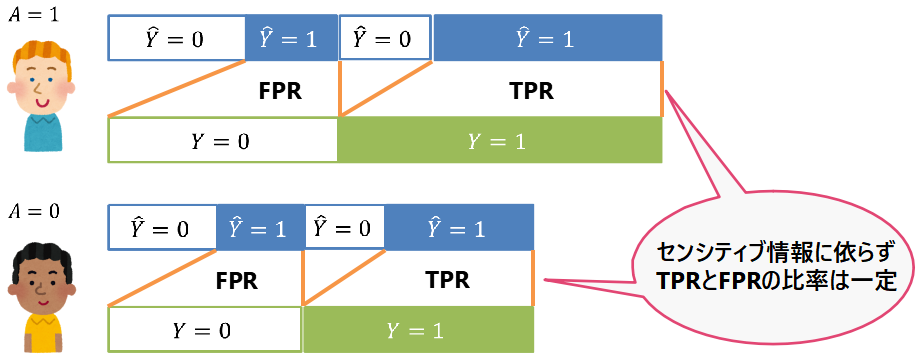
■公平性の定義：等価オッズ
事例：再犯予測プログラムCOMPAS
COMPASについては第1章の事例1でも取り上げました。１つ目の問題点は、2年以内に再犯しなかった（$Y=0$）人の中で、再犯すると予測（$hat{ Y }=1$）された人の割合（誤検知率）が人種により異なることでした。すなわち、アフリカ系アメリカ人は白人よりも2倍ほど誤検知率が高いのです。2つ目の問題点は、2年以内に再犯した（$Y=1$）人の中で、再犯しないと予測（$hat{ Y }=0$）された人の割合（見逃し率）が人種により異なることでした。 誤検知率は偽陽性率$P(hat{ Y } = 1| Y = 0)$と一致し、見逃し率は$1$から真陽性率$P(hat{ Y } = 1| Y = 1)$を引いたものであることに注意すると、人種間で真陽性率（TPR）および偽陽性率（FPR）が一致することで本事例の問題を解決できそうです。定義（等価オッズ）：
予測ラベル$hat{ Y }$、センシティブ属性$A$、目的変数$Y$に対して、
$P(hat{ Y } = 1| A = 1, Y = 1) = P(hat{ Y } = 1| A= 0, Y = 1)$ …（TPRの相等）
$P(hat{ Y } = 1| A = 1, Y = 0) = P(hat{ Y } = 1| A= 0, Y = 0)$ …（FPRの相等）
が成り立つとき、等価オッズを満たすという。
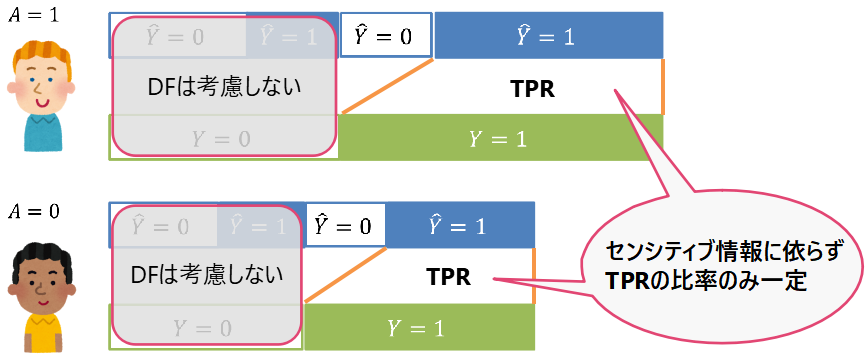
■公平性の定義：機会均等
事例：ローンリスク
ローンの融資の場面を考えましょう。主な融資対象者は債務不履行を起こさない人（$Y=1$）なので、そのような顧客に対しては公平性を要求し、債務不履行（DF）を起こした人（$Y=0$）には公平性を考慮しない運用を行ったとします。すなわち、DFを起こさない人にのみ、センシティブ属性に依らないローン融資の機会が均等にあるべきだという基準です。定義（機会均等）：
予測ラベル$hat{ Y }$、センシティブ属性$A$、目的変数$Y$に対して、
$P(hat{ Y } = 1| A = 1, Y = 1) = P(hat{ Y } = 1| A= 0, Y = 1)$ …（TPRの相等）
が成り立つとき、機会均等を満たすという。
これは等価オッズの定義を緩めたもので、属性間で真陽性率のみ一致することを要請しています。逆に、等価オッズは機会均等よりも厳しい公平性規準と言えます。一般に公平性と精度はトレードオフの関係にあるので、シナリオごとに何を優先し、どの公平性規準を採用するのかを設計する必要があります。
不公平性の緩和
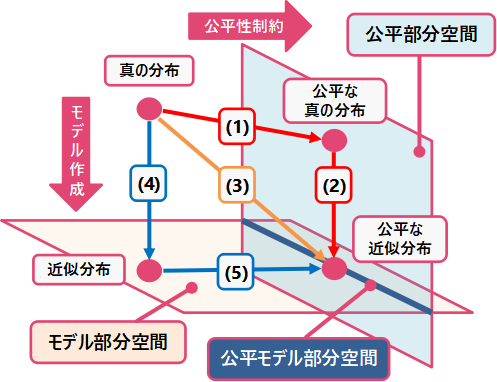しかし、真の分布からサンプリングされたと考えることができる実データを手に入れることは可能だが、現実世界に存在する差別のために、”公平な真の分布”というものは存在せず、もちろん公平な実データを手に入れることもできません。したがって、図中(1)で現実的に行えることは、真の分布からサンプリングされた実データが公平性を満たすように前処理することです。この前処理されたデータをもとに分類器を作成することで公平な分類器を獲得できます（図中(2)）。このほかにも、実データから直接公平な分類器を作成する方法や（図中(3)）、実データから分類器を作成し（図中(4)）、公平性制約を満たすように補正する（図中(5)）方法なども提案されています。これらのアプローチを下表にまとめました。| 対処法 | 説明 |
|---|---|
| Pre-processing（前処理） | 不公平な可能性のあるデータを公平なデータに変換し(1)、これを用いて分類器を作成する(2)。 分類器についての仮定を導入せずに、公平部分空間への適切な射影を決めるのには困難が伴う。 |
| In-processing（中処理） | 公平なモデルは、不公正な可能性のあるデータから直接学習される(3)。 分類器の設計に自由度があるが、目的関数の定式化や、最適化には技術的な困難が伴う。 |
| Post-processing（後処理） | 分類器を最初に学習し(4)、公平性制約を満たすようにこの分類器を補正する(5)。 紛失性（公平な予測結果が非センシティブ属性に依存しない）を仮定すると補正が容易となる（後述）。 |
■Pre-Processing（前処理）
前処理では、クラス分類の結果に影響しない範囲で入力データを変換します。マッサージング：
マッサージングは学習用データの目的変数を書き換える前処理です。最初に、公平性を考慮せずに作成した標準的な分類器を作成します。この分類器を用いて学習用データの各レコードに正例（y=1）になりやすさのスコアを付与します（また、負例はy=0とします）。このスコアに基づいてセンシティブ属性ごとに学習用データを整列させます。スコアに対してある閾値を定め、スコアが閾値以上であれば正例、そうでなければ負例に振り分けるように予測スコアをラベル化します。この閾値は予測ラベルの比率がセンシティブ属性間で同一となるように定めます。下図では、センシティブ属性に依らずに予測ラベルの比率が1:1となるように閾値を定めました。最後に、閾値未満にある正例を負例に、閾値以上にある負例を正例に変換します。変換後の学習用データで再度分類器を学習させることで、公平な分類器を獲得できます。用いる分類器のアルゴリズムが変換の前後で異なる場合には最適な結果が得られない可能性があるので注意が必要です。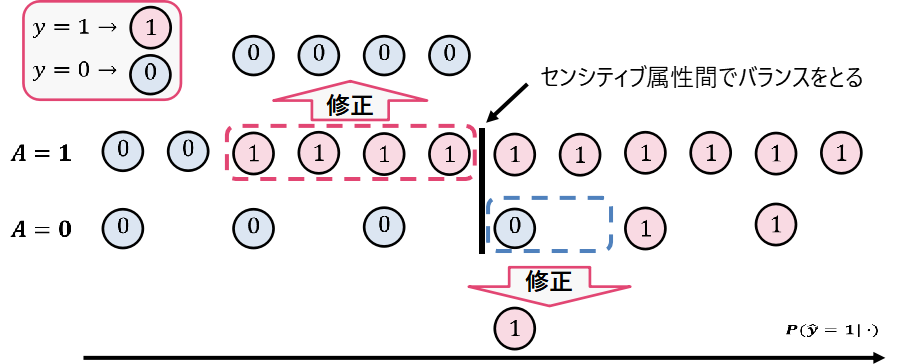
参考文献：Data preprocessing techniques for classification without discrimination
■In-Processing（中処理）
中処理では、学習の際に目的関数や制約条件に公平性を満たす処置を施します。正則化法：
正則化法は、目的関数にモデルの公平性のための正則化項を付け加えた上で最小化する方法です。正則化法のアルゴリズムで学習パラメータを得るためには、下記の式を計算します：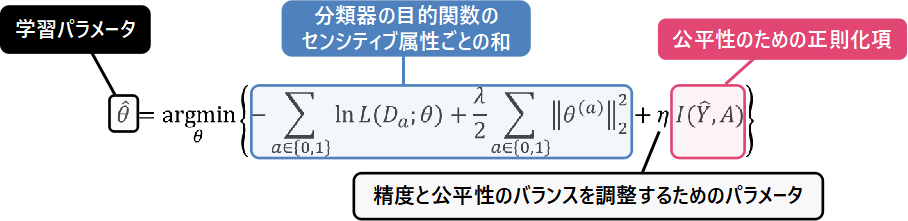
青枠で表した部分は過学習を防ぐための正則化項を付け加えた目的関数です。ピンク色の枠で表した部分が公平性のための正則化項です。$eta$を調節することで公平性の強度を調節することが可能です。また、公平性のための正則化項としてはとの独立性を測る相互情報量などが用いられます：
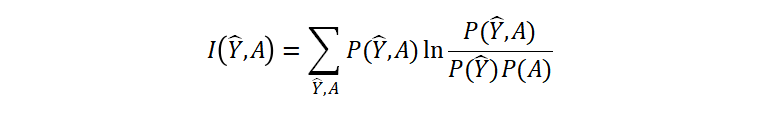公平性のための正則化を付けた目的関数は凸関数と凹関数の和となるため、最適化を行う際に困難が伴います。
参考文献：Fairness-aware Classifier with Prejudice Remover Regularizer
無相関制約による最適化問題：
$hat{ Y }$と$A$との独立性ではなく無相関性に条件を緩め、この条件を最適化問題の制約条件として課す方法です。無相関制約による最適化アルゴリズムで学習パラメータを得るためには、下記の式を計算します：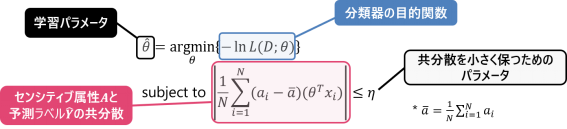
ここで$N$はデータの総数を表します。また、青枠で表した部分の目的関数は負の対数尤度です。ピンク色の枠で表した部分が公平性のための制約条件で、$hat{ Y }$と$A$の共分散の絶対値を十分小さくせよ、という制約を表しています。$eta$を調節することで公平性の強度を調節することが可能です。
参考文献：Fairness Constraints: Mechanisms for Fair Classification
■Post-Processing（後処理）
後処理では、公平性を考慮せずに作成した分類器から得られた予測ラベルや予測スコアを公平性が満たされるように修正します。Post hoc補正：
Post hoc補正では、不公平な可能性のあるモデルを用いて予測したラベルまたはスコアを公平性を満たす新たな予測ラベルへ変換する補正器を作成します。後述する紛失性というやや強めの仮定を導入することで、学習用データを再学習することなく補正するができます。 Post hoc補正の手順は以下の通りです。まず、公平性を考慮していない事前のモデルから目的変数$Y$を予測する2値のラベルあるいは実数値のスコア（確率値だと考えて構わない）を作成し、これを$hat{ Y }$とします。次に、$hat{ Y }$を公平性を満たすラベルへ変換する補正器$tilde{ Y }$を作成します。この補正器は、下記の紛失性を満たす関数の中から探索します。定義（紛失性）：
関数$tilde{ Y }$が、$hat{ Y }$、$A$および$Y$にのみに依存するとき、すなわち、$tilde{ Y }=tilde{ Y }(hat{ Y },A,Y)$となるときに$tilde{ Y }$は紛失性を満たすという。
上記の紛失性の定義では、目的変数$Y$の依存性を考慮しました。以下では、$Y$への依存性を考慮しないので、$tilde{ Y }=tilde{ Y }(hat{ Y },A)$という形の補正器を扱います。今後は、この形で表示された補正器を紛失性を満たすということにします。
紛失性の意味を考えてみましょう。$hat{ Y }$を作成する際に使用したモデルは、非センシティブ属性$X$やセンシティブ属性$A$で構成される説明変数と目的変数$Y$を用いて学習します。紛失性とは、補正器$tilde{ Y }$が非センシティブ属性$X$に依存しないことを要求しています。これは、事前のモデル作成過程に依存せず（その過程を忘れてしまって）、手持ちの予測ラベルあるいはスコア$hat{ Y }$とセンシティブ属性$A$があれば公平性のためのpost hoc補正が行えることを意味しています。
Post hoc補正によるアルゴリズムで補正器を探索するためには、下記の制約条件付き最適化問題を解きます：
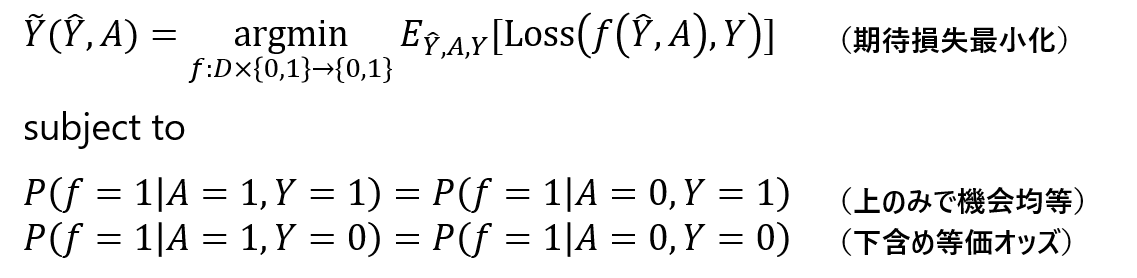
ここで、$D$は、$hat{ Y }$が予測ラベルならば$D=${0,1}とし、$hat{ Y }$が予測スコア、特に確率値ならば$D=$[0,1]などと適宜読み替えます。また、$Loss(・,・):${0,1}$× ${0,1}$ → R$は損失関数を表します。
関数$f$の形に制限を加えることで、上記の最適化問題を最適な閾値を求める問題に書き換えてみましょう。$hat{ Y }$は確率値の予測スコアとします。また、このスコアに対してセンシティブ属性$A$に依存した閾値$T(A)$を導入します。このとき、$f$を
$f(hat{ Y },A)=1(hat{ Y } geq T(A))$
の形で表しましょう。ここで、$begin{eqnarray}1(prop)
=
begin{cases}
1 prop:True \
0 prop:False
end{cases}
end{eqnarray}$です。すると、上記の最適化問題は以下のような閾値最適化問題に書き換えられます：
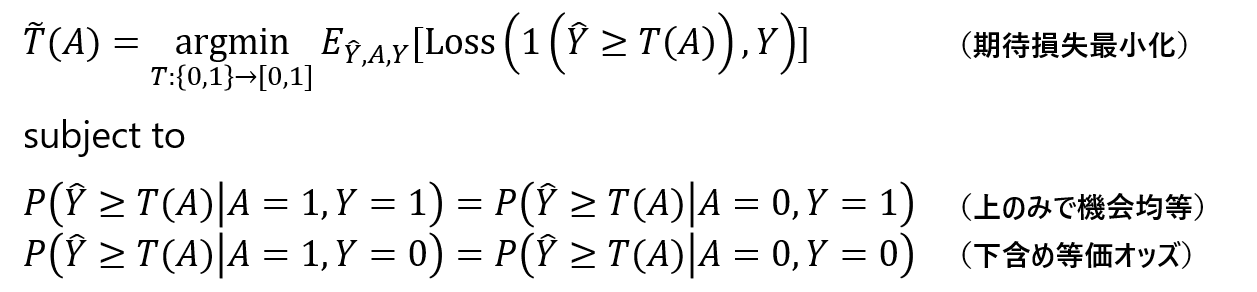
これらの閾値最適化問題に関しては、Attacking discrimination with smarter machine learningの中でわかりやすくグラフィカルなシミュレーションが取り上げられています。
参考文献：Equality of Opportunity in Supervised Learning
参考文献：Learning Non-Discriminatory Predictors
