差分の差分法(理論編)

今回は差分の差分法という手法を解説します。
理論編と実装編に分けての解説になります。

1.はじめに

ビジネスにおいて何らかの施策を行ったときにその効果を検証することは重要です。施策の結果の良し悪しにもとづいて、施策を継続する、あるいは施策を中止して改善策を検討するといった意思決定を行う必要があるためです。しかし、データに潜むバイアスを考慮せずに施策の効果検証を行うと、施策の効果を過大評価/過小評価してしまう場合があります。

ここからは当社が得意とするマーケティングを例にとり解説をします。ある小売店の店舗（以下店舗Aとします）に対して値下げ施策による売上の増大効果を考えます。このとき、施策によってどれだけ売上が増加したかを評価するにはどうすればよいでしょうか。まず考えられるのは、施策を行った店舗Aと施策を行っていない別の店舗Bで売上を比較する方法です。この方法では、店舗Aと店舗Bの売上の差分を施策の効果と見做します。しかし、その差分には本来の施策の効果に加えて、店舗ごとのもともとの売上の違いが含まれるため、施策の効果を正しく評価できているとはいえないでしょう。次に考えられるのは、店舗Aの施策開始後と開始前の売上を比較する方法です。この方法では、店舗Aの施策開始後と開始前の売上の差分を施策の効果と見做します。店舗Aの売上データのみを使って効果検証を行うため、先程の方法での問題点を回避できそうです。しかし、例えば、施策開始後にSNSで偶然話題になった（値下げ施策を打ったこととは全くの無関係に偶然話題になった）商品が飛ぶように売れたなど、施策とは全く別の要因で売上が変化した可能性があると、仮に施策開始後に売上が増加していたとしても、それがすべて施策の効果だとはいえないでしょう。

上記のような誤った方法で効果検証を行うと、本当は効果が小さい施策を過大評価してしまって継続判断となり効果に見合わない運用コストを払う、あるいは本当は効果が大きい施策を過小評価してしまって中止判断となり機会損失が生じる、といった由々しき事態を招くおそれがあります。こういった事態を回避するために、因果推論と呼ばれる手法を活用することが考えられます。今回の記事では、因果推論の手法の1つである差分の差分法を紹介します。

 

2.差分の差分法とは

2.1差分の差分法の考え方

前節では施策の効果検証として、店舗毎の比較と施策を行った店舗の施策開始前後の比較を行うことの問題点を説明しました。この節では、それぞれの問題点に対処する「差分の差分法」を紹介します。差分の差分法は、店舗毎に施策開始前後の比較を行い、その結果を店舗間で比較するという手法になります。
前節の説明から、店舗Aの施策開始前後の売上の差の要因は、「施策の効果」と「施策以外の要因による効果」に分けられます。このことは、
（店舗Aにおける施策開始後の売上）–（店舗Aにおける施策開始前の売上）=（施策の効果）＋（施策以外の要因による効果）    (1）
という数式として表現出来ます。式(1)の「施策以外の要因による効果」は、店舗Aにおいて仮に施策を行わなかった場合の売上の変化として現れます。
図1に 式(1)のイメージを示しました。

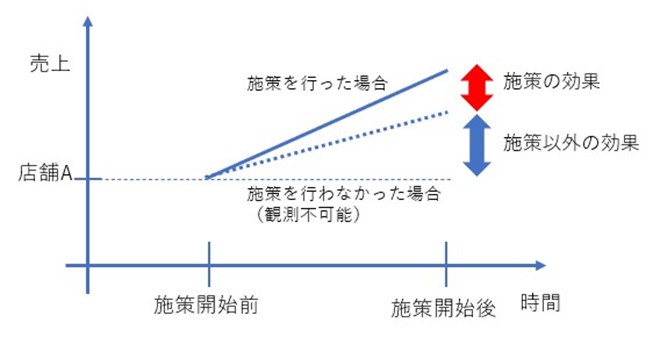
図１

「施策の効果」を評価するためには、店舗Aの売上の施策開始前後の売上比較の結果から、「施策以外の要因による効果」を除く必要があります。しかし、実際には店舗Aに施策を行ったので、施策を行わなかった場合（if）の売上は観測することができないため、「施策以外の要因による効果」を求めることはできません。
そこで「施策以外の要因による効果」を、施策を行わなかった他の店舗Bから推定することを考えます。店舗Aで仮に施策を行わなかった場合の売上変化が、店舗Bにおける売上変化と同じであると仮定します。つまり「施策以外の要因による効果」が店舗AとBで共通であると仮定します。これは「平行トレンドの仮定」と呼ばれ、差分の差分法を用いる際は重要な仮定となります。平行トレンドの仮定のイメージを図2に示しました。

店舗Bの売上変化を式で表すと、以下のようになります。

（店舗Bにおける施策開始後の売上）–（店舗Bにおける施策開始前の売上）=（施策以外の要因による効果）   (2）
以上を踏まえると、「施策の効果」は式(1)と式(2)の両辺を引いて得ることができます。
（施策の効果）={（店舗Aにおける施策開始後の売上）–（店舗Aにおける施策開始前の売上）}-{（店舗Bにおける施策開始後の売上）–（店舗Bにおける施策開始前の売上）}

以上のように、店舗Aと店舗Bそれぞれの売上の施策開始前後で差分を取り、さらにそれらの店舗間で差分を取ることから、この手法は「差分の差分法」と呼ばれます。

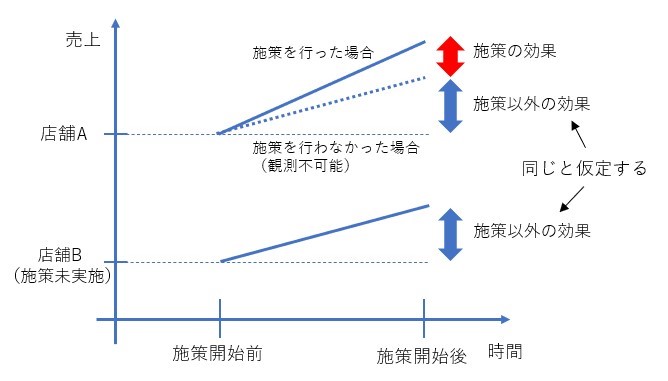
図2

2.2平行トレンドの仮定の確認方法

差分の差分法では平行トレンドの仮定が成り立つことが大前提となります。しかし、店舗Aに仮に施策を行わなかった場合の売上は観測不可能なため、実際に平行トレンドの仮定を立証することはできません。その代わりとして、平行トレンドの仮定が成り立っていることを間接的に確認する方法を2点紹介します。
1つ目は、処置開始前の期間のデータを用いて店舗Aと店舗Bの間で平行トレンドの仮定が成立することを確認する方法です。店舗A・Bそれぞれの売上トレンドを時系列プロットとして可視化し、両プロットの形状が大きく食い違っていないことを確認します。両プロットの形状がどの程度似通っていれば平行トレンドの仮定が成立していると言ってよいかは難しい問題ですが、大きく食い違っていない（平行トレンドの仮定が明らかに不成立とはいえない）ことを確認することは出来ます。処置開始前にこの仮定が成り立っていたとしても、処置開始後に何らかの要因で仮定が崩れる可能性はあります。しかし、処置開始前に平行トレンドの仮定が成立することは、処置開始後にもこの仮定が成立する可能性を示唆する最低限の条件となります。

２つ目は、施策開始以降の期間に一方の店舗のみに影響する出来事の有無を調査することです。例えば、店舗Bの近くに競合店が新しくオープンしたといったことがあれば、そのことが原因で店舗Bの売上が減少してしまうかもしれません。そのような出来事がないかどうかを確認することも、平行トレンドの仮定が成立することを検証する上では必要です。
なお、店舗Aと店舗B両方に同じ程度に影響を与える出来事は「共通ショック」といいますが、特に対処する必要はありません。共通ショックが起こっても平行トレンドの仮定には影響を及ぼさないためです。

上記２つの方法はどちらも分析の際に必ず確認すべき事項ですが、他にも平行トレンドの仮定を崩してしまいそうな要因があれば、すべて確認することが重要です。

3.差分の差分法を用いた線形回帰モデル

3.1線形回帰モデルの定式化

この節では、差分の差分法の考え方にもとづいた線形回帰を行う方法を紹介します。
まず準備として、因果推論の用語をいくつか説明します。まず小売店における施策などの何らかのアクションのことを処置と呼びます。そして処置を行った店舗を処置群、処置を行わなかった店舗を対照群といいます。さらに、売上など、処置によって影響を受ける変数を結果変数\(Y\)以上をもとに線形回帰モデルを定式化します。まず処置開始前を時刻\(t=0\) 、処置開始後を\(t=1\) とします。時刻\(t\)はある期間が処置開始後か否かを表すダミー変数とも解釈できます。次に、時刻\(t\)の店舗\(i\)の結果変数（売上）\(Y_{it}\)と表します。また、店舗\(i\)が処置群であるか否かを表すダミー変数を\(d_i\)とします。このとき、線形回帰モデルは以下のように表されます。

\(Y_{it}\)=\(α_i\)+\(β_t\)\(t\)+\(β_{dt}\)\(d_i\)\(t\)+\(ε_{it}\)　　　（3）

ただし\(ε_{it}\)は誤差項（E[\(ε_{it}\)]＝0が成り立つとします）としています。

3.2線形回帰モデルの各項の解釈

式(3)の線形回帰式の各項の係数は以下のように解釈されます。
まず、式(3)において処置開始前（\(t=0\) ）の場合の売上\(Y_{it}\) の期待値を取ると、
E[\(Y_{i0}\)]＝\(α_i\)
となり、定数項\(α_i\)は店舗\(i\)の処置開始前の売上ということがわかります。

次に\(β_t\)についてですが、対照群（ \(d_i\)=0）の店舗\(i\)における処置開始後（\(t=1\)）と処置開始前（\(t=0\)）の売上\(Y_{it}\)の差分の期待値を取ると、
E[\(Y_{i1}\)-\(Y_{i0}\)]＝\(β_t\)

となります。上式左辺は対照群の店舗の売上変化の期待値であるため、上式は係数\(β_t\) が「処置以外の要因による効果」を表しているといえます。

さらに、処置群（ \(d_i\)=1）の店舗\(i\) における処置開始後（\(t=1\)）と処置開始前（ \(t=0\)）の売上\(Y_{it}\)の差分の期待値を取ると、
E[\(Y_{i1}\)-\(Y_{i0}\)]＝\(β_t\)+\(β_{dt}\)
となります。上式左辺は処置群の店舗の売上変化の期待値を表しており、また係数\(β_t\) は処置群においても「処置以外の要因による効果」を表すので（ここで平行トレンドの仮定を用いています）、係数\(β_{dt}\)が「処置効果」を表していることがわかります。

式(3)のイメージを図で表すと、図3のようになります。

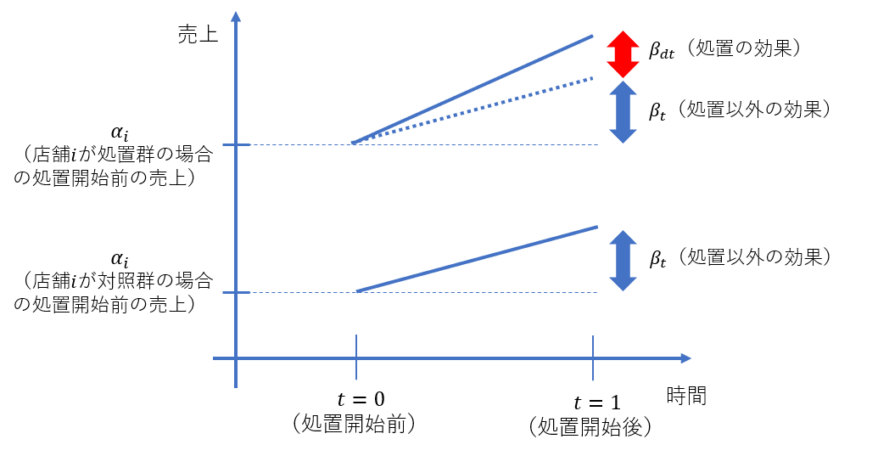
図３

理論編は以上になります。お読み頂きまして大変有難うございました。次回は実装編です。是非合わせてお読み頂ければ幸いです。

参考文献
・安井翔太, 効果検証入門, 技術評論社.
・西山慶郎 他, 計量経済学, 有斐閣.
・Matt Taddy（原著）, 上杉隼人 他（訳）, ビジネスデータサイエンスの教科書, すばる舎.
・伊藤公一朗, データ分析の力 因果関係に迫る思考法, 光文社.
・岩波データサイエンス刊行委員会編, 山口慎太郎, 岩波データサイエンス Vol.3 “差の差法で検証する「保育所整備」の効果―社会科学における因果推論の応用”, 岩波書店.
・Joshua D. Angrist 他（原著）, 大森義明 他（訳）, 「ほとんど無害」な計量経済学―応用経済学のための実証分析ガイド, NTT出版.