差分の差分法の実装編になります。
実装編本文中の数式は理論編のものとなります。理論編を合わせて御確認頂けますと幸いです。
理論編はこちら
4.Pythonによる実装
4.1データの準備
まずはモジュールをインポートします。
|
1 2 3 4 5 6 |
# モジュールのインポート import pandas as pd import numpy as np import matplotlib import matplotlib.pyplot as plt import statsmodels.api as smf |
次にデータの準備をしていきます。今回は人工的に店舗の売上データを作成します 。ここでは架空の店舗A~Dの2022年4月~12月の月別売上を考えます。ここで、店舗A、Bを処置群、店舗C、Dを対照群とします。また4~9月を処置開始前、10~12月が処置開始後期間とすることにします。まず各店舗の各年月の全組み合わせのデータを生成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 店舗名と年月の全組合せのデータを作るため、クロスジョインを行う。 # 店舗データ dm_pre1 = pd.DataFrame( data = {'店舗名':['A', 'B', 'C', 'D'], # クロスジョイン用のキー 'key':1} ) # 年月データ dm_pre2 = pd.DataFrame( data = {'年月':['2022-04', '2022-05', '2022-06', '2022-07', '2022-08', '2022-09', '2022-10', '2022-11', '2022-12'], # クロスジョイン用のキー 'key':1} ) dm = pd.merge(dm_pre1, dm_pre2) # 不要なカラムの削除 dm.drop("key", axis=1, inplace=True) |
次に各店舗の売上のデータを作成します。まず各店舗の処置開始前の売上はそれぞれ異なっているとします。また各店舗の売上変化の大きさは店舗の規模に比例すると考えます。つまり、例えば処置効果としては、「売上が何万円増加したか」というよりも、「売上が何%増加したか」というように比率として考えるということです。
処置開始前には系統的な変動はないとし、処置開始後に各店舗に「処置以外の要因による効果」が共通に加わり(共通ショック)、さらに処置群の店舗にのみ「処置効果」が加わるとします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# 各店舗の施策開始前の売上を設定 dm["A"] = 120 dm["B"] = 80 dm["C"] = 100 dm["D"] = 50 # 店舗A,Bを処置群に、店舗C,Dを対照群に store_treated = ["A", "B"] store_control = ["C", "D"] # 処置開始月を2022年10月にする month_start = "2022-10" # 処置以外の効果を売上20%増加、処置効果を売上30%増加として設定 dm["処置以外の効果"] = 1.2 dm["処置効果"] = 1.3 # 各店舗の売上の確率的な変動として、各売上の値を±7.5%する np.random.seed(1) rand = np.random.rand(36)* 0.15 + 0.925 rand_Series = pd.Series(rand) dm["rand"] = rand_Series # 処置群の各店舗の月別売上の計算。 for i in store_treated: # 処置開始前 dm.loc[((dm["店舗名"] == i) & (dm["年月"] < month_start)), "月別売上(円)"] = dm[i] * dm["rand"] # 処置開始後 dm.loc[((dm["店舗名"] == i) & (dm["年月"] >= month_start)), "月別売上(万円)"] = dm[i] * dm["処置以外の効果"] * dm["処置効果"] * dm["rand"] # 対照群の各店舗の月別売上の計算。 for i in store_control: # 処置開始前 dm.loc[((dm["店舗名"] == i) & (dm["年月"] < month_start)), "月別売上(万円)"] = dm[i] * dm["rand"] # 処置開始後 dm.loc[((dm["店舗名"] == i) & (dm["年月"] >= month_start)), "月別売上(万円)"] = dm[i] * dm["処置以外の効果"] * dm["rand"] # 不要なカラムの削除 dm.drop(["A", "B", "C", "D", "処置以外の効果", "処置効果", "rand"], axis=1, inplace=True) # 作成したデータマートの先頭15行を表示 print(dm.head(15)) |
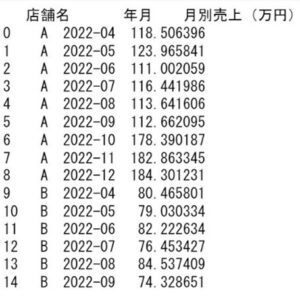
4.2データの前処理・可視化
この小節ではデータの前処理及び可視化を行っていきます。
まず目的変数である売上を対数に変換します。
前小節で設定した通り、各店舗の売上変化の大きさは店舗の規模に比例するとしているため、売上を対数に変換することで、売上変化を比率で捉えます。
|
1 2 3 |
# 売上を対数に変換 dm.loc[:,"月別対数売上(万円)"] = dm.loc[:,"月別売上(万円)"].apply(np.log10) dm.drop("月別売上(万円)", axis=1, inplace=True) |
次にデータの可視化を行い、平行トレンドの仮定が問題ないかの確認を行います。
|
1 2 3 4 5 6 7 8 |
# 売上の縦持ちデータを横持ちデータに直す dm_sale = dm.pivot_table(values=['月別対数売上(万円)'], index=['年月'], columns=['店舗名'], aggfunc='sum', fill_value=0) # matplotlibの設定 matplotlib.rc('font', **font) # 各店舗の月別の対数売上のプロット dm_sale['月別対数売上(万円)'].plot(y=['A', 'B', 'C', 'D'], ylabel='月別対数売上(万円)', ylim=[1.5,2.4], yticks=[1.5, 1.8, 2.1], grid=True, figsize=(10,5), alpha=1) |
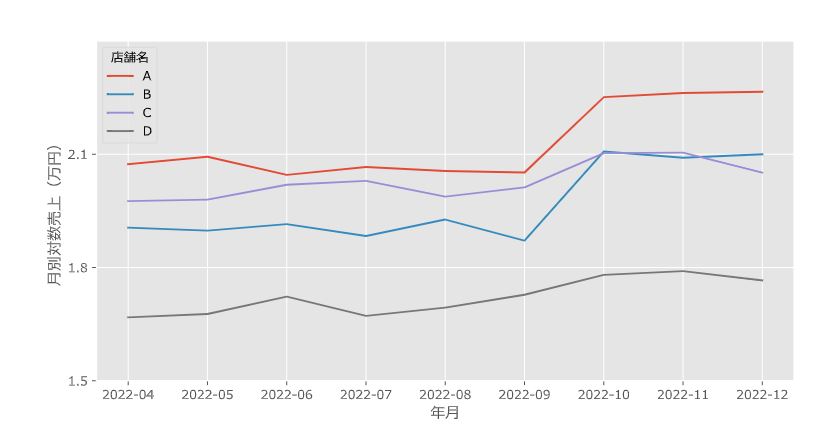
今回はデータを人工的に用意したため、平行トレンドの仮定が成り立っていることはわかっているのですが、手順の確認のため2.2節で説明した方法を踏まえてチェックをします。 1つ目の方法として、処置開始前のデータ(2022年4月-2022年9月)において平行トレンドの仮定が成り立っているかを確認します。 ここでは目視で確認しますが、どの店舗の売上もほぼ横ばいになっており、平行トレンドの仮定が成り立っているように見えます。 また2.2節の2つ目の方法である、一部の店舗のみに影響した出来事の確認ですが、これは基本的に売上データだけからはわからないため、ここでは確認できません。実際の分析ではドメイン知識に基づいて該当する出来事がないか調べることになります。今回はそのような出来事は存在しないという設定とします。
ここからは線形回帰モデルの実装のための前処理を行っていきます。 まず線形回帰モデル(式(3))の第1項に対応させ、各店舗のダミー変数を導入します。これらのダミー変数の係数が、各店舗の処置開始前における売上(ここでは対数売上)\(α_i\)に相当します。
|
1 2 3 4 5 |
# 店舗名をダミー化 dummy = pd.get_dummies(dm.loc[:, "店舗名"]) dm_dummy = pd.concat([dm,dummy], axis = 1) # '店舗名'カラムを削除 dm_dummy.drop('店舗名', axis=1, inplace=True) |
そして、各店舗が処置群であるか否かを表すダミー変数(式(3)における\(d_i\)に相当します)及び、
各期間が処置開始後か否かを表すダミー変数で(式(3)における\(t\)に相当します)をそれぞれ導入します。
|
1 2 3 4 5 6 7 8 9 10 |
# 処置群ダミーの導入 dm_dummy["処置群ダミー"] = 0 dm_dummy.loc[((dm_dummy["A"] == 1) | (dm_dummy["B"] == 1)), "処置群ダミー"] = 1 # 期間ダミーの導入 dm_dummy["期間ダミー"] = 0 # 処置開始月は2022年10月 month_start = "2022-10"dm_dummy.loc[dm_dummy["年月"] >= month_start, "期間ダミー"] = 1 # "年月"カラムの削除 dm_dummy.drop("年月", axis=1, inplace=True) |
|
1 2 3 4 |
# 期間ダミー変数×処置群ダミー変数の導入 dm_dummy["期間ダミー×処置群ダミー"] = dm_dummy["期間ダミー"].copy() * dm_dummy["処置群ダミー"].copy() # 処置群ダミーの削除 dm_dummy.drop("処置群ダミー", axis=1, inplace=True) |
4.3線形回帰モデルによる推定
この小節では線形回帰モデルを実装し、処置効果の推定を行っていきます。|
1 2 3 4 5 |
# 目的変数と説明変数に分ける dm_Y = dm_dummy["月別対数売上(万円)"] dm_X = dm_dummy.drop("月別対数売上(万円)", axis=1) # 線形回帰モデルの学習 model = smf.OLS(dm_Y,dm_X) |
|
1 2 3 |
# 線形回帰モデルの分析結果 result = model.fit() result.summary() |
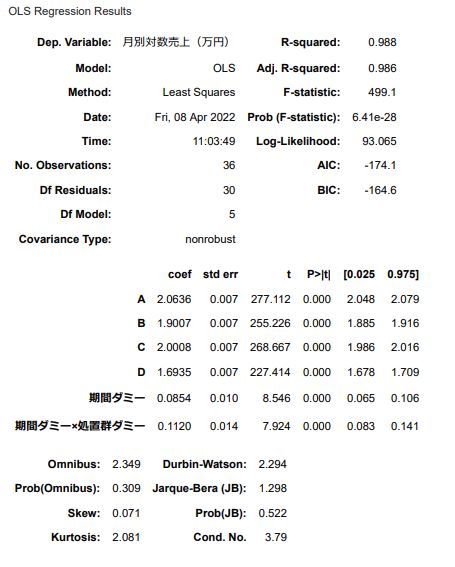
推定結果の確認は以下の3つの流れで行います。
① 線形回帰モデルの精度について確認
② 線形回帰モデルの各係数が有意かどうかを確認
③ 回帰係数を用いて処置効果の推定
まず①についてですが、ここではモデルの当てはまりの良さを表す決定係数Rを確認します。決定係数の値が低い場合はモデルの当てはまりが悪いことを意味しており、線形回帰で推定した係数が信用出来ないため、処置効果の推定することが出来ません。今回のケースでは1に非常に近くなっていることがわかります。今回は各店舗 の施策開始前の売上 を線形回帰モデルに入れましたが、このような場合は決定係数が1に近くなることが多いです。あくまで目安程度に見るのが良いでしょう。
次に②に関して、回帰モデルの各係数を確認します。各係数の意味としては、ダミー変数A~Dの係数(式(3)における\(α_i\))は各店舗の処置開始前の対数売上を、期間ダミー変数の係数(式(3)における\(β_t\))は「処置以外の要因による効果」を、そして期間ダミー×処置群ダミー変数の係数(式(3)における\(β_{dt}\))は「処置の効果」を表しています。各係数のp値はどれも0.05を下回っており、統計的に有意(各係数の推定値は偶然そのような値になったとは言えないと見なしてよい)といえます。
最後に③の「処置効果」の推定として、期間ダミー変数×処置群ダミー変数の係数の値を確認します。推定値は0.112、標準誤差が0.014となっています。元のスケールに戻すと、推定値は10^0.112≅1.294で、95%信頼区間は[10^(0.1200-1.96⋅0.014),10^(0.1200+1.96⋅0.014)]≈[1.238,1.404]となります。
従って、処置により売上は29.4%(信頼区間は23.8%~40.4%)増加していると推定できます。今回の人工データでは処置効果を30%と設定していたので、精度良く推定できていることがわかります。
4.4差分の差分法と単純集計による推定結果の比較
4節の締めとして、1節で問題提起した「バイアスを考慮しない単純な効果推定」を実際に執り行い、差分の差分法の推定結果と比較することで、差分の差分法の有効性を確認します。ここで、比較対象となる「バイアスを考慮しない単純な効果推定」は集計ベースで行うため、そこに合わせて差分の差分法を集計ベースで行います(差分の差分法は集計ベースでも行うことができます)
以下では売上の近い処置群の店舗Aと対照群の店舗Cのデータのみを使って集計することにします(それぞれの施策開始前の売上は、店舗Aでは120万円、店舗Cでは100万円です)。
このとき、上記の①店舗比較による推定②施策前後の比較による推定③差分の差分法に基づく推定の方法はそれぞれ以下のようにまとめられます:
①(店舗比較による処置効果の推定)=(店舗Aにおける処置開始後の平均売上)-(店舗Cにおける処置開始後の平均売上)
②(前後比較による処置効果の推定)=(店舗Aにおける処置開始後の平均売上)-(店舗Aにおける処置開始前の平均売上)
③(差分の差分法による処置効果の推定)={(店舗Aにおける処置開始後の平均売上)-(店舗Aにおける処置開始前の平均売上)}-{(店舗Cにおける処置開始後の平均売上)-(店舗Cにおける処置開始前の平均売上)}
それでは上記の推定を実装していきます。まず集計に必要な前処理を行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
# 店舗Bと店舗Dの売上レコードを削除 dm_AC = dm_dummy.copy() dm_AC.drop(dm_AC[(dm_AC["B"] == 1) | (dm_AC["D"] == 1)].index, inplace = True) # 店舗Aか否かのダミー変数と期間ダミー変数以外のカラムを削除する。 dm_AC.drop(["B", "C", "D", "期間ダミー×処置群ダミー"], axis=1, inplace=True) # 平均売上の計算 ## 店舗・期間ごとの売上の平均値を計算 mean = dm_AC.groupby(["A", "期間ダミー"], as_index=False)["月別対数売上(万円)"].mean() ## 店舗Aの施策開始後の平均売上 sale_storeA_after = mean.loc[(mean["A"]==1) & (mean["期間ダミー"]==1)]["月別対数売上(万円)"].iloc[-1] ## 店舗Aの施策開始前の平均売上 sale_storeA_before = mean.loc[(mean["A"]==1) & (mean["期間ダミー"]==0)]["月別対数売上(万円)"].iloc[-1] ## 店舗Cの施策開始後の平均売上 sale_storeC_after = mean.loc[(mean["A"]==0) & (mean["期間ダミー"]==1)]["月別対数売上(万円)"].iloc[-1] ## 店舗Cの施策開始前の平均売上 sale_storeC_before = mean.loc[(mean["A"]==0) & (mean["期間ダミー"]==0)]["月別対数売上(万円)"].iloc[-1] # 平均売上の誤差分散の計算 ## 店舗・期間ごとの平均売上の誤差分散を計算 lambda_squared_error = lambda x: x.var()/x.count() squared_error = dm_AC.groupby(["A", "期間ダミー"], as_index=False)["月別対数売上(万円)"].apply(lambda_squared_error) ## 店舗Aの施策開始後の平均売上の誤差分散 error_storeA_after = squared_error.loc[(squared_error["A"]==1) & (squared_error["期間ダミー"]==1)]["月別対数売上(万円)"].iloc[-1] ## 店舗Aの施策開始前の平均売上の誤差分散 error_storeA_before = squared_error.loc[(squared_error["A"]==1) & (squared_error["期間ダミー"]==0)]["月別対数売上(万円)"].iloc[-1] ## 店舗Cの施策開始後の平均売上の誤差分散 error_storeC_after = squared_error.loc[(squared_error["A"]==0) & (squared_error["期間ダミー"]==1)]["月別対数売上(万円)"].iloc[-1] ## 店舗Cの施策開始前の平均売上の誤差分散 error_storeC_before = squared_error.loc[(squared_error["A"]==0) & (squared_error["期間ダミー"]==0)]["月別対数売上(万円)"].iloc[-1] |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 店舗比較:(店舗Aの施策開始後の平均売上)と(店舗Cの施策開始後の平均売上)の差分 sale_diff_storeA_C = sale_storeA_after - sale_storeC_after # 店舗比較の誤差分散:(店舗Aの施策開始後の平均売上)と(店舗Cの施策開始後の平均売上)の差分の誤差分散 # 平均値の差の誤差分散を、それぞれの平均値の誤差分散の和として計算する error_diff_storeA_C = error_storeA_after + error_storeC_after # 誤差分散を標準誤差に直す se_diff_storeA_C = np.sqrt(error_diff_storeA_C) # 処置効果の推定値と標準誤差を表示 print(sale_diff_storeA_C) print(se_diff_storeA_C) |

出力結果から、店舗比較による推定値はおよそ10^0.174≅1.493で、95%信頼区間は[10^(0.174-1.96⋅0.018),10^(0.174+1.96⋅0.018)]≈[1.376,1.619]となります。つまり処置効果は約49.3%(信頼区間は37.6%~61.9%)と推定されます。 実際の処置効果は30%であるため、処置効果が過大に推定されています。これは店舗Aと店舗Cの処置開始前の売上の違い(店舗Aでは120万円、店舗Cでは100万円です)が反映されていると考えられます。 次に②同一店舗における処置開始の前後比較を行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 前後比較:(店舗Aの施策開始後の平均売上)と(店舗Aの施策開始前の平均売上)の差分 sale_diff_storeA = sale_storeA_after - sale_storeA_before # 前後比較の誤差分散:(店舗Aの施策開始後の平均売上)と(店舗Aの施策開始前の平均売上)の差分の誤差分散 # 平均値の差の誤差分散は、それぞれの平均値の誤差分散の和として計算する error_diff_storeA = error_storeA_after + error_storeA_before # 誤差分散を標準誤差に直す se_diff_storeA = np.sqrt(error_diff_storeA) # 処置効果の推定値と標準誤差を表示 print(sale_diff_storeA) print(se_diff_storeA) |

出力結果から、店舗Aの施策前後比較による推定値はおよそ10^0.195≅1.567で、95%信頼区間は [10^(0.195-1.96⋅0.008),10^(0.195+1.96⋅0.008)]≈[1.511,1.624]となります。従って処置効果は約56.7%(信頼区間は51.1%~62.4%)と推定されます。 実際の処置効果は30%であるため、処置効果は過大に推定されています。これは処置開始後には、処置以外の要因による売上変化(売上20%増加)があるためと考えられます。 最後に③の差分の差分法を行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 店舗Aの前後比較:(店舗Aの施策開始後の平均売上)と(店舗Aの施策開始前の平均売上)の差分 sale_diff_storeA = sale_storeA_after - sale_storeA_before # 店舗Cの前後比較:(店舗Cの施策開始後の平均売上)と(店舗Cの施策開始前の平均売上)の差分 sale_diff_storeC = sale_storeC_after - sale_storeC_before # 差分の差分法:(店舗Aの前後比較)-(店舗Cの前後比較) sale_diff_diff = sale_diff_storeA - sale_diff_storeC # 店舗Aの前後比較の誤差分散:(店舗Aの施策開始後の平均売上)と(店舗Aの施策開始前の平均売上)の差分の誤差分散 error_diff_storeA = error_storeA_after + error_storeA_before # 店舗Cの前後比較の誤差分散:(店舗Cの施策開始後の平均売上)と(店舗Cの施策開始前の平均売上)の差分の誤差分散 error_diff_storeC = error_storeC_after + error_storeC_before # 差分の差分法の誤差分散:(店舗Aの前後比較)-(店舗Cの前後比較)の誤差分散 # (店舗Aの前後比較)と(店舗Cの前後比較)の値が正規分布に従うと近似し、正規分布の分散の加法性を用いる error_diff_diff = error_diff_storeA + error_diff_storeC # 誤差分散を標準誤差に直す se_diff_diff = np.sqrt(error_diff_diff) # 処置効果の推定値と標準誤差を表示 print(sale_diff_diff) print(se_diff_diff) |

結果を見ると、差分の差分法による推定値はおよそ10^0.110≅1.288で、95%信頼区間は[10^(0.110-1.96⋅0.021),10^(0.110+1.96⋅0.021)]≈[1.171,1.416]となります。従って処置効果は約28.8%(信頼区間は17.1%~41.6%)と推定されます。実際の処置効果は30%であり、精度良く推定できていることがわかります。
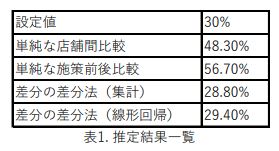
以上の結果を表1に整理します。バイアスを考慮せずに単純に集計した結果と、差分の差分法で推定した結果を比較すると、差分の差分法による推定結果がより良く効果を推定出来ていることが分かります。
なお、上記推定値は4.3節で線形回帰モデルにより得られた値(29.4%)と比べると少し精度が劣っており、また標準誤差も0.021であり線形回帰モデルの場合(0.014)よりも大きくなっています。これは、本小節では店舗Aと店舗Cのデータのみを使っており、すべての店舗データを使った線形回帰モデルの場合と比べてサンプル数が減っているためと考えられます。
5.まとめと参考文献
差分の差分法の解説は以上となります。今回はマーケティング施策の効果検証を例として、差分の差分法を解説致しました。今後も施策の効果検証を適切に行うための方法を紹介していく予定ですので、施策効果検証の実務に携わる方々のご参考になれば幸いです。
参考文献
・安井翔太, 効果検証入門, 技術評論社.
・西山慶郎 他, 計量経済学, 有斐閣.
・Matt Taddy(原著), 上杉隼人 他(訳), ビジネスデータサイエンスの教科書, すばる舎.
・伊藤公一朗, データ分析の力 因果関係に迫る思考法, 光文社.
・岩波データサイエンス刊行委員会編, 山口慎太郎, 岩波データサイエンス Vol.3 “差の差法で検証する「保育所整備」の効果―社会科学における因果推論の応用”, 岩波書店.
・Joshua D. Angrist 他(原著), 大森義明 他(訳), 「ほとんど無害」な計量経済学―応用経済学のための実証分析ガイド, NTT出版.




