生産計画を数理最適化問題として解く！現場実装のための業務要件に合わせたチューニングとは？

数理最適化問題としての生産計画

生産計画は、効率的な製品生産を実現するためにたいへん重要な業務です。昨今、生産計画にAI・数理最適化を導入することが注目されています。この記事では、AI・数理最適化の技術要素についてご紹介します。

こちらの記事もぜひご覧ください。
▶生産計画最適化とは？生産計画にAI・数理最適化を導入する３つのメリットを解説！
▶生産計画最適化を事例で解説！よくある課題と解決策とは？

生産計画問題（Production Planning Problem）

生産計画は、部品や原材料などの入荷状況や製品の納期など複雑な条件を考慮しつつ、コストの最小化や利益の最大化などを目的として、製品の生産量などを計画する数理最適化問題として扱うことができます。ここでは、例題として以下のような設定の生産計画問題を、数理最適化問題として考えます。

数理最適化問題としての定式化

この問題を数理最適化問題として定式化、つまり数式として表現してみましょう。定式化の際は、以下の観点で要件を整理することがポイントになります。

まず、この問題では「どの製品をいつ、どれだけ生産し、倉庫の在庫を確保するか」が決めたいことになります。数理最適化のフレームワークでは、決めたいことを変数として定義しますが、この変数のことを決定変数と呼びます。

また、最適化の目的は「コスト（＝生産費と在庫費の合計）を最小にする」ことになります。最適化によって最小化（もしくは最大化）したい数式のことを目的関数と呼びます。

そして、主な制約条件は以下の通りです。

• 製品を生産するための原材料の消費量が、原材料の供給量を超えないこと
• 前週から持ち越した在庫量と当該週の生産量から、当該週の需要量を差し引いたものが、当該週の在庫量に一致すること
• 製品の生産量および在庫量は0以上であること

 

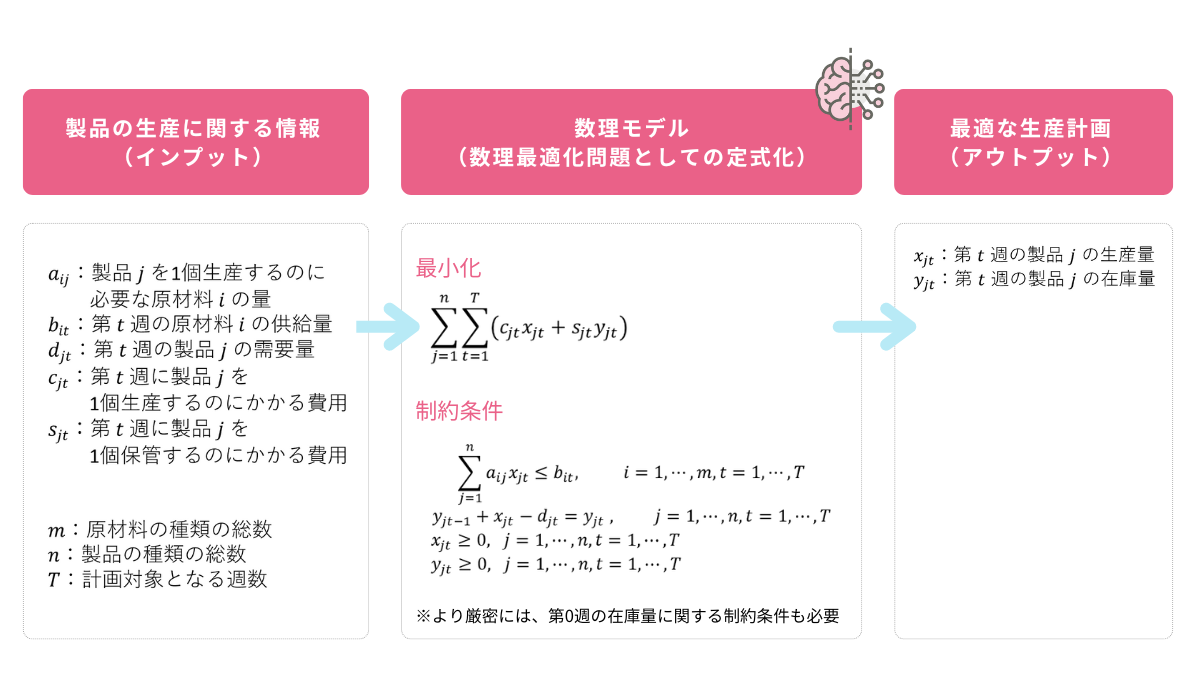
これらの要件を数式で表現すると、下図のようになります。

図中の左に示しているのが、今回の生産計画に必要なインプット情報であり、図中央下の制約条件を満たすように、図中央上のコストを最小化するように数理最適化問題を解きます。
結果として、図右の生産量および在庫量として最適な値（解と呼びます）を求めることができます。
数式の詳細な点までご理解いただけなくても、数理最適化のイメージを掴んでいただければと思います。

実務で数理最適化を活用する際は、要件を数式で表現したものを、数理最適化問題を解くための専用のソフトウェア（ソルバーと呼ばれます）を使って実装し、それを実行することで解を求め、生産計画の策定に活用します。

業務要件に合わせたチューニング

制約条件や目的関数のチューニング

要件を整理する際にいちばん難しいのは、制約条件を明確化することです。作業としては、お客様からヒアリングした業務要件をひとつひとつ数式として表現していくことになりますが、はじめからすべての制約条件を網羅的に洗い出すことは難しいでしょう。

ある程度制約条件を数式で表現できたら、いまの制約条件のもとで最適化問題を解いて得られる解を見てみて、業務に即した現実的な解になっているかを検証する作業が必要になります。
この検証結果を受けて制約条件をブラッシュアップし、再度最適化問題を解いて得られた解を検証する、というサイクルを繰り返し、実用に足る生産計画の策定を目指すのが、数理最適化の導入の一般的な流れです。
今回の問題例でいうと、「製品の生産量および在庫量は0以上であること」という制約条件は、生産現場の方からすれば当たり前のことであるため見落としがちですが、得られた解を検証した結果、生産量がマイナスの解が得られたことがわかれば、この制約条件を追加する必要があることが明確になります。

また、制約条件などの要件を整理する過程で、どういうデータが必要なのかも整理されるため、どういったデータを整備する必要があるかも明らかになります。
さらに、生産計画において所与としているが計画策定時には確定値が不明であるもの（たとえば需要量）をAIによる予測で求めたい場合は、そのためのデータ整備や予測モデルの構築も併せて検討していきます。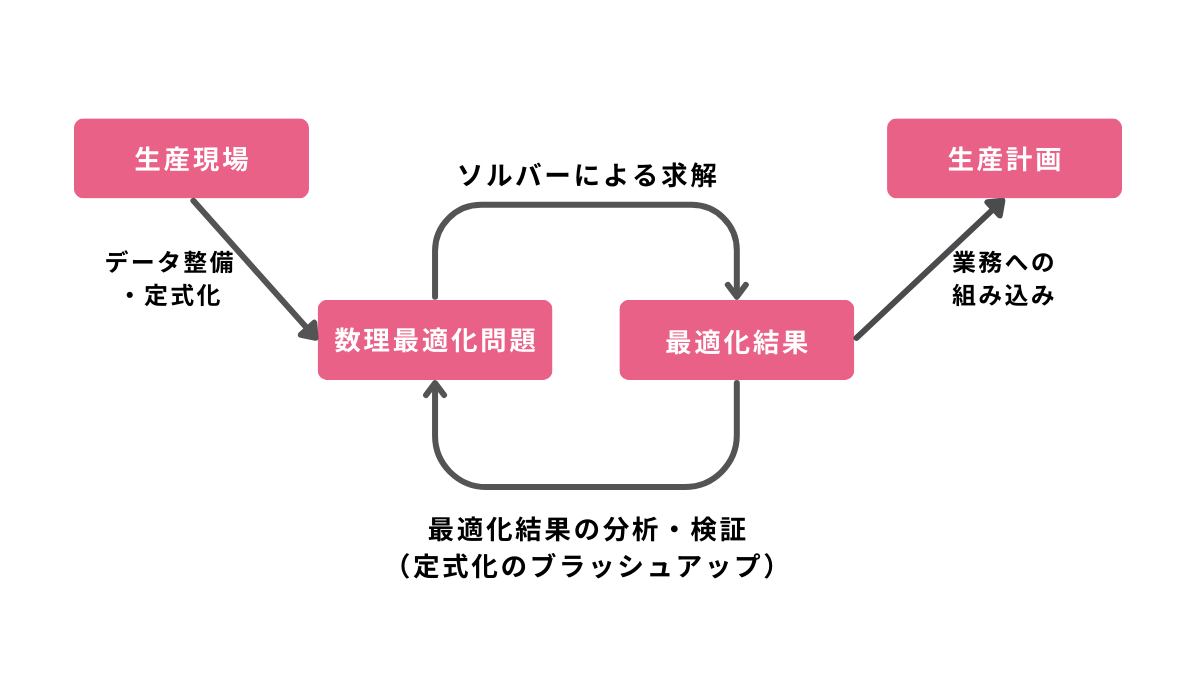

今回ご紹介した生産計画問題はあくまで一例であり、お客様の業務要件や事業で目指す姿に応じてその定式化は変わります。たとえば、コストを最小化することよりも、利益を最大化することに興味がある場合は、最適化の目的をコスト（＝生産費と在庫費の合計）の最小化から、利益の最大化に変更することができます。この場合、製品を1個生産した際に得られる利益などのインプット情報を用意する必要があります。

求解方法のチューニング：解の精度と計算時間のバランスの考慮

数理最適化のフレームワークでは、決めたいことを決定変数として定義することをご紹介しました。

たとえば、「どの製品をいつ、どれだけ生産するか」を決めたい場合、「特定の製品を特定の時期に生産する量」を表す決定変数を用意します。多品種の生産計画を策定する必要がある場合や、長期の計画を策定する必要がある場合、決定変数の数が増えることがわかるかと思いますが、決定変数の数が増えるほど計算時間は長くなることに注意が必要です。

数理最適化のフレームワークでは、決定変数の数が倍になれば計算時間が倍になるのではなく、指定した制約条件を満たす解の組合せを求めるため、さらに多くの計算時間がかかる可能性があります。たとえば、早朝に計画策定に必要なデータの連携がなされ、1営業日内に生産計画を策定しなければならないとき、数理最適化の計算に2営業日かかってしまうようでは、数理最適化を業務に導入することは現実的ではないでしょう。

そのような場合、メタヒューリスティクスと呼ばれる近似解法を使って解を求める方法もあります。この方法は、解の精度は若干下がる（たとえば、コスト最小化を目指す場合、得られた解ではコストが理論的な最適値を上回る）場合がある一方で、比較的短い時間で解を求められる特徴があります。

この方法を使う場合についても、実際にどのような解が得られるかを検証したうえで、解の精度が許容できるか、その解が現実的かどうか、また業務フローに組み込めるだけ計算時間が短いかなどのバランスを考慮し、求解方法を設計することが重要です。

まとめ

ここまで、生産計画へのAI・数理最適化の導入について、技術的な側面に着目してご紹介しました。

生産計画の最適化、AI導入にもしご興味をお持ちでしたら、ぜひお気軽にご相談、お問い合わせください！TDSEの専門チームが、お客様の具体的なニーズに合わせたソリューションをご提案いたします。