A/Bテストの概要(マーケター向け)
A/Bテストとは
「ウェブサイトのレイアウトを変更して、売上が逆に落ちてしまい後悔する」
「ウェブサイトに新しい機能を追加したが、ユーザーがどのような反応するか心配になる」
などを経験したことがありますでしょうか。このような状況を防ぐには、A/Bテストを行うことが重要です。
A/BテストとはAバージョン、Bバージョンと別々のウェブページを用意し、どちらのバージョンのコンバージョン率が高いかを比較する手法です。例えば、Microsoftが提供する検索エンジンのBingでは、広告のヘッドライン表示を変更した際に、A/Bテストを実施しました。具体的には、ランダムに選ばれた一部のユーザーには新しいタイトルレイアウトを表示し、それ以外のユーザーには古いタイトルレイアウトを表示させることで、新しいタイトルレイアウトの効果を検証しました。このA/Bテストを実施したことにより、1億ドル以上の利益を上げることができたようです。
なぜA/Bテストを行う必要があるか
A/Bテストを行うことによって、新しいウェブサービスをリリースする際に効果が落ちてしまうリスクを抑えることができるからです。
A/Bテストを用いて、新しいウェブサービスを一部のユーザーだけに表示させ、事前に反応を確認することで、新しいサービスをリリースする時に効果が落ちるリスクを抑えることができます。また、問題が生じた場合でもすぐリカバリーすることができます。
A/Bテストの結果の信頼性を高めるために
A/Bテストの結果の信頼性を高めるために、以下のことをチェックする必要性があります。
1)A/Bテストに必要な日数の適切な設定
A/Bテストを実施する前に、適切な期間を設定することが重要です。
A/Bテストの期間を必要以上に長く設定すると、コストがかかります。逆に、A/Bテストの期間を必要以上に短く設定すると、判断する上で有用な結論が得られなくなることがあります。特に近年はリーンスタートアップが主流となってきており、A/Bテストと改善のサイクルを高速で回していくことが求められていますので、A/Bテストを実施する期間を適切に設定することはより重要になっていくと思われます。
当社のお客様でもA/Bテスト期間の設定にお悩みの方が多いため、簡単に見積もるツールを作成し、社内で活用しています(近日公開予定)。A/Bテストの設計・実施をお悩みの方は、ぜひ当社にお問い合わせください。
A/Bテスト実施の必要日数計算ツール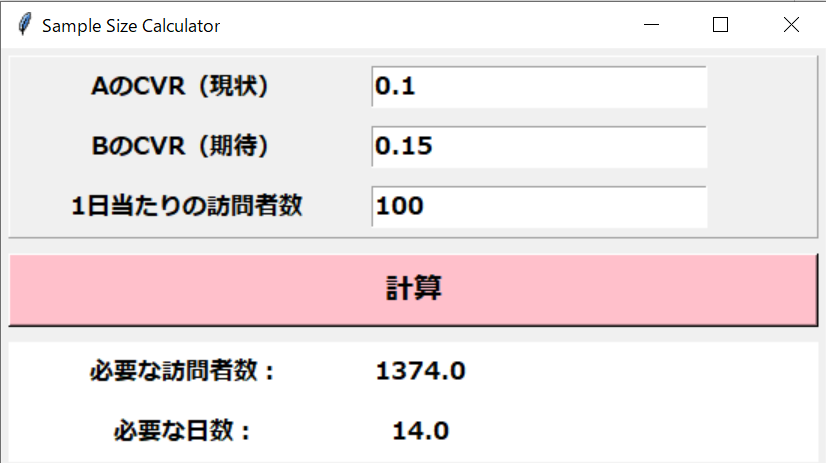
検定:カイ二乗検定、P値:0.05、検定力:0.8で設定している
2)実施したA/Bテストの検定力の確認
A/Bテストを実施した後、どの程度の検定力のもとで行われたか確認する必要があります。検定力が低い場合、統計的に「バージョンAとバージョンBに差がない」という結論になったとしても、実際に「バージョンAとバージョンBに差がない」とは限らなくなります。この場合は、より大きな検定力でA/Bテストを再度実施する必要があります。 検定力の定義について後ろに記載しています。
A/Bテストに必要な統計学
カイ二乗検定
A/Bテストでよく使われる独立性の検定について紹介します。独立性の検定とは2つの属性に関連があるかを検定することです。例えば、ウェブサイトのデザインとコンバージョンに関連があるかどうかを検証したい場合は独立性の検定を用います。カイ二乗分布という確率分布を利用する場合は、カイ二乗検定とも呼ばれます。
カイ二乗検定で帰無仮説H0と対立仮説H1は以下のように定義されます。
H0:二つの変数は独立である
H1:二つの変数は独立ではない(関連があるということ)
カイ2乗検定で使用する統計検定量は、下記の式で与えられる$χ²$となります。

ここで、$O_1$,…,$O_k$は観測度数、$E_1$,…,$E_k$は期待度数です。観測度数は実際の度数で、例えば、実際のコンバージョンした件数です。期待度数は二つの変数は独立であるという帰無仮説のもとで、帰無仮説が正しければこれくらいの度数を取るだろうと期待される度数のことです。$χ²$値によって、観測度数($O_1$,…,$O_k$)と期待度数($E_1$,…,$E_k$)の間のずれを評価します。
カイ二乗検定で通常、以下の手順でやっていきます。
例えば、ウェブサイトのデザインを検討するためのA/Bテストを実施し、以下のようなデータが得られたとします。
実験1:
| コンバージョン した件数 |
コンバージョン しなかった件数 |
コンバージョン率 | |
| デザインA | 50 | 50 | 50% |
| デザインB | 60 | 40 | 60% |
実験1でウェブサイトのデザインとコンバージョンに関連があるかどうかを検証するには、カイ二乗検定を行います。
①帰無仮説として「ウェブサイトのデザインとコンバージョンは独立である(関連はない)」という仮説を立てます。
②統計検定量($χ²$)を計算してから、P値(後述)を計算します。
実験1のP値を計算すると、「0.15」になります。
③P値で帰無仮説を棄却するかどうか判断します。
ここで、有意水準(帰無仮説を棄却する基準)を0.05に設定します。実験1ではP値(=0.15)>0.05となるので帰無仮説を棄却できないことになります。
P値
P値とは、帰無仮説が正しいもとで計算された検定統計量が、実際の観測値から求めた値以上に極端な値をとる確率のことです。P値が小さいほど、検定統計量がその値となることは起こりえなくなります。P値の大小を判断する基準を有意水準(帰無仮説を棄却する基準)とよびます。P値が有意水準以下の場合には帰無仮説を偽として棄却し、対立仮説を採択します。一般的に有意水準は0.05に設定することが多いです。
検定力
仮説検定では、第一種の過誤と第二種の過誤を考慮します。第一種の過誤とは帰無仮説が真であるのにもかかわらず、帰無仮説を偽として棄却してしまう誤りのことです。第一種の過誤を犯す確率は通常αと表します。第二種の過誤は帰無仮説が偽であるにもかかわらず、それを真として棄却しない誤りのことです。第二種の過誤を犯す確率をβと表します。
| 実の結果 | |||
| 帰無仮説が正しい | 対立仮説が正しい | ||
| 検定の結果 | 帰無仮説を採択 | 正しい 確率:1 – α |
第二種の過誤 確率:β |
| 帰無仮説を棄却 | 第一種の過誤 確率:α |
正しい 確率:1 – β |
|
検定力とは本当に違いがある場合に帰無仮説を棄却する確率のことで、検定力=1 – βとなります。
検定力を算出することで、検定結果の信頼性を知ることができます。もし検定力が小さい場合、第二種の過誤を犯している可能性が高いことから、本当は有意差があるのに差がないと判断されてしまいます。通常、検定力は0.8に設定します。
信頼性の高いA/Bテストを行うために
事前にサンプルサイズを設計する
サンプルサイズが大きくなるにつれて、$χ²$の値は大きくなります。するとP値が小さくなるので、帰無仮説を棄却しやすくなります。つまり、実質的に差がなくても、サンプルサイズが大きくなると、「有意差あり」という結論を付けやすくなってしまいます。逆に、サンプルサイズが小さい場合は、$χ²$の値も小さくなり、実際に差があっても帰無仮説を棄却しないと結論づけるおそれがあります。こういったことを防ぐために、適切なサンプルサイズを計算する必要があります。
サンプルサイズは検定力、有意水準などを事前に決めておくと、Rのpwr.chisq.testといったパッケージやpythonのstatsmodels.stats.power.GofChisquarePowerといったライブラリを利用して求めることができます。
検定力を確認する
第二種の過誤を防ぐために、A/Bテストを実施した後に、どの程度の検定力のもとで行われたか確認する必要があります。
検定力は、サンプルサイズ、有意水準などからRのpwr.chisq.testといったパッケージやpythonのstatsmodels.stats.power.GofChisquarePowerといったライブラリを利用して計算することができます。
■参照文献
・Ron Kohavi , Diane Tang , Ya Xu,『A/Bテスト実践ガイド』大杉直也訳, ドワンゴ.
・野口 竜司,A/Bテストの教科書, マイナビ出版.
・”統計WEB 統計用語集:P値”, https://bellcurve.jp/statistics/glossary/2172.html ,(参照 2021-4-28).
・”統計WEB 統計用語集:検定力”, https://bellcurve.jp/statistics/course/12767.html ,(参照 2021-4-28).
・”統計WEB 統計用語集:第二種の過誤”, https://bellcurve.jp/statistics/glossary/1781.html ,(参照 2021-4-28).




